Monte Carlo Szimuláció

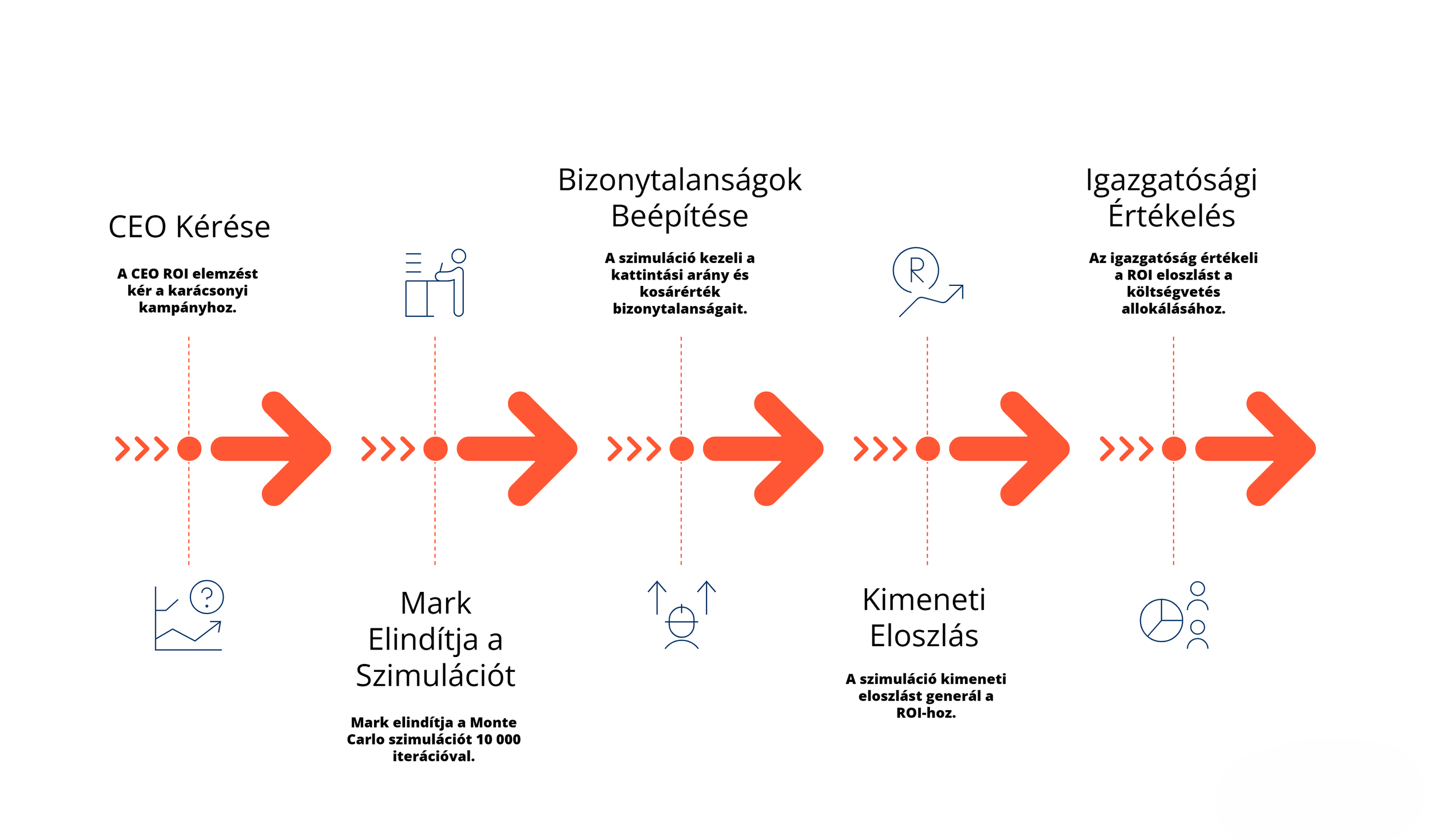
Szerdán Mark Etman épp az ebédjét falja a tárgyalóban, amikor Daniel Ross, a CEO, bedob egy PowerPoint-ot:

“Mark, a karácsonyi kampány ROI-ját szeretném látni konfidencia-intervallumokkal: mi a worst-case, mi a best-case, és mi a legvalószínűbb forgatókönyv. Holnap reggelig legyen készen!”

Mark felkészül, elindítja a Monte Carlo-szimulációt 10 000 iterációval a kattintási arány és kosárérték bizonytalanságaival. Másnap a board megnézheti a megtérülés-sűrűségfüggvényt, és biztonsággal (vagy bizonyos kockázattal) allokálhatja a büdzsét.

Nézzük, mi az a Monte Carlo simulation, és miért nélkülözhetetlen a kockázat­alapú marketingtervezésben.

0. Mi az a Monte Carlo simulation?

Véletlensokaságon alapuló iteratív számítás, amely bemeneti eloszlásokból kimeneti eloszlást képez.

1. Miért jó?

• Bizonytalanság modellezése: lehetővé teszi, hogy változók eloszlása mentén többszörös szcenáriót vizsgáljunk.

• Rugalmasság: bármilyen valószínűségi eloszlást használhatunk (normál, log-normal, egyenletes, stb.).

• Kimeneti eloszlás: nemcsak egy pontbecslést, hanem a kimeneti eredmény valószínűségi eloszlását is megkapjuk.

• Döntéstámogatás: konfidencia-intervallumok, kockázati mutatók kiszámítására is alkalmas.

• Teljes kockázati spektrumot ad

• Nem csak egy pontbecslést, hanem konfidencia-intervallumot is

2. Hogyan számítható?

• Bemeneti eloszlások meghatározása: minden bizonytalan változóról kiválasztunk egy statisztikai eloszlást és paramétereket (átlag, szórás stb.).

• Véletlen mintavétel: minden inputból generálunk egy-egy értéket a meghatározott eloszlás szerint (pl. =NORM.INV(RAND(); átlag; szórás)).

• Modell futtatása: az így kapott értékeket betápláljuk a kalkulációs képletbe vagy modellbe, és kiszámoljuk a kimenetet.

• Ismétlés: a fenti 2–3. lépést ezerszám vagy tízezerszám végrehajtjuk, minden iterációban új véletlen mintát használva.

• Eredmények összegzése: a kimeneti eredményekből hisztogramot készítünk, és kiszámoljuk az átlagot, mediánt, konfidencia-intervallumokat.

3. Mikor használd?

• Komplex modellek esetén, ahol zárt alakú megoldás nincs vagy nehéz.

• Nagy bizonytalanság mellett (pl. inputok széles eloszlása).

• Kockázatelemzésnél: worst-case, best-case és legvalószínűbb kimenetek feltárására.

• Projekttervezésben (PERT-típusú), pénzügyi előrejelzésben, készlet- és kapacitástervezésben.

4. Marketing-példák

• Kampány-ROI szimuláció: email-, display- és social-spend bizonytalan hatásának vizsgálata.

• Eladás-előrejelzés: napi forgalom szóródásának modellezése a szezonális ingadozásokkal együtt.

• CLTV-becslés: vásárlási gyakoriság és kosárérték véletlenszerű ingadoztatása az élettartam-érték eloszlásához.

• Árkockázat: kedvezményes árstratégiák hatásának szimulációja különböző versenypiaci feltételek mellett.

5. Case Study: havi bevétel-szimuláció

1. Bemenet:

   Átlagos forgalom = 500 000 Ft, havi szórás = 50 000 Ft (normál eloszlás)

   E-mail kampány konverziós arány = 8 % ±2 % (normál eloszlás)

2. Függvény Excelben minden iterációhoz:

   Bevetel = NORM.INV(RAND(); 500000; 50000)

   CR = NORM.INV(RAND(); 0.08; 0.02)

3. Megtérülés = (Bevetel * CR * ÁtlagosKosárÉrték) / KampányKöltség

4. Szimuláció: 10 000 iteráció → 10 000 ROI-érték.

5. Eredmény:

   ROI átlaga, 95 %-os konfidencia-intervallum: [1,2×; 1,6×]

   Kockázatjelző: 5 % alatti ROI-k aránya ≈ 8 %.

6. Döntés: ha a vállalat csak ROI ≥ 1,5×-et fogad el, a szimuláció alapján a kampányt 65 % valószínűséggel indítsa.

6. Mikor ne használd?

• Kismintás adatoknál (néhány tíz vagy száz megfigyelés), mert a véletlen fluktuáció torzíthat.

• Determinisztikus modellek esetén, ahol nincs többféle kimenet (logisztikus regresszió diszkrét válaszának helyett).

• Számítási korlátok: nagyon nagy iterációszám esetén hosszú futási időt igényelhet.

• Input eloszlások ismeretének hiányában: ha pontatlanul határozzuk meg az inputok eloszlását, a kimeneti eloszlás is félrevezető lesz.

7. Milyen üzleti kérésekre adhat választ?

• A CFO azt kéri, “Mutasd meg, milyen ROI-eloszlás jön ki, ha kattintási arányunk és kosárértékünk is ingadozik” – hogyan építed fel a szimulációt?

• A kampánytervezésnél szeretnél 95%-os konfidencia-intervallumot a bevételre – hány iteráció kell, és mit mutat ez?

• Ha egyszerre a display, social és email költés is bizonytalan, hogyan döntöd el, hol spóroljunk?

• A marketing vezető kíváncsi, mennyire “riogasson” a worst-case forgatókönyv – hogyan adod meg?