Likelihood (sigmoid p)

Péntek reggel Penny Sellmore home officeban a kávéját és a reggeli müzlit élvezi, miközben a Slacken átfutja a CRM dashboardot (na persze). Hirtelen megcsörren a Zoom. Penny eszeveszetten rohan vissza a teraszról. A CEO, Robert Miller hívja. A képernyőn a főnöke arca látszik:

“Penny, a következő e-mail kampányunknál szeretném, ha csak azokat a leadeket céloznánk, akiknek legalább 70% esélyük van vásárlásra. A marketingbüdzsé szűkös, nem lehet rossz találgatásokra pazarolni. ASAP küldj egy listát!”

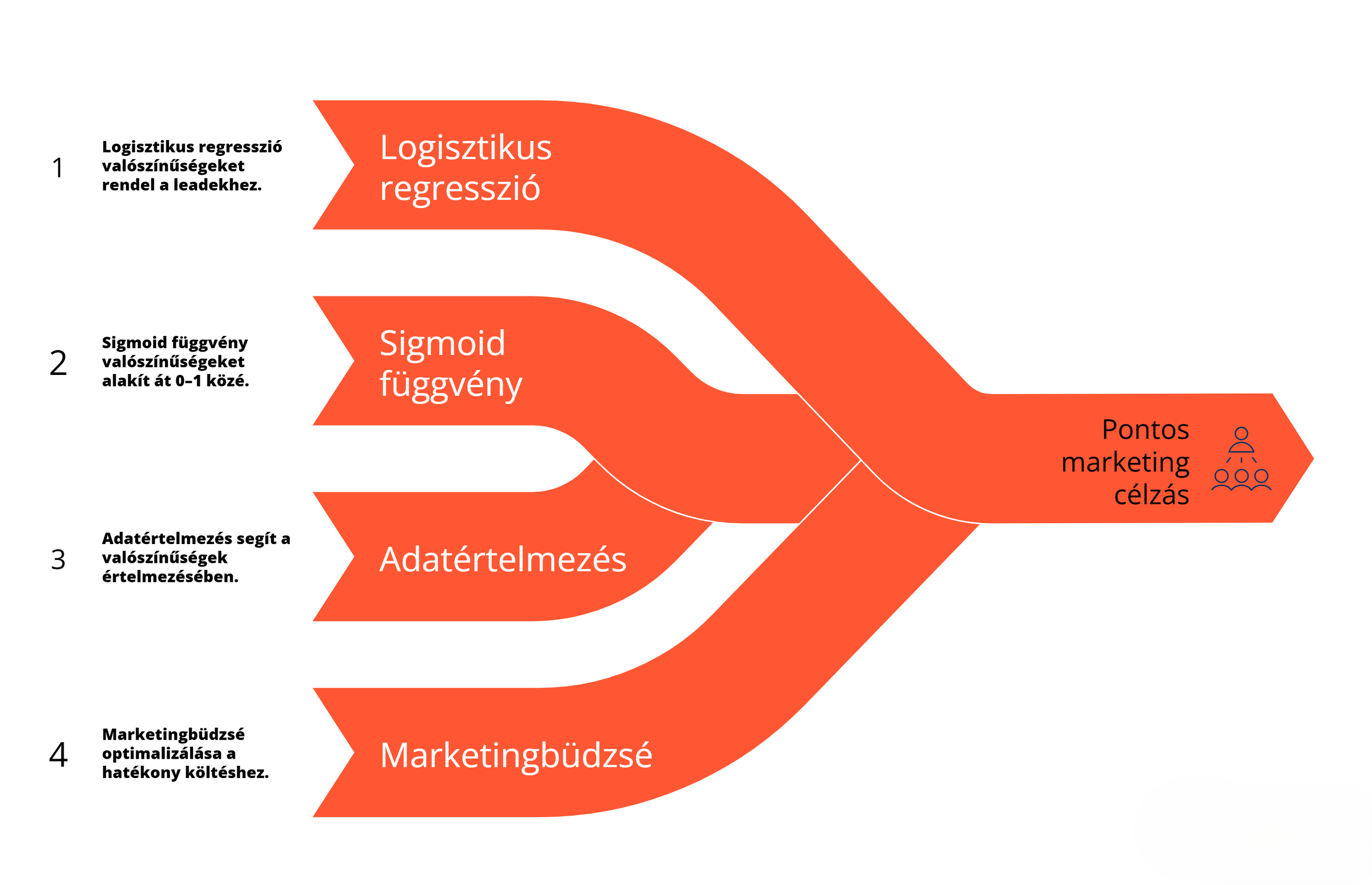
Penny elmosolyodik: „Ez aztán a reggel!” Gyors korty a kávéból, behűti a müzlit, és már kattint is a modelljére. A logisztikus regresszió sigmoid függvényével minden leadhez 0–1 közti valószínűséget rendel, így csak a 0.7 feletti p-értékűeket exportálja. Most már pontosan tudja, kikre érdemes költeni a kampánybüdzsét.

Nézzük, mit takar a sigmoid transzformáció, és miért nélkülözhetetlen marketingben.

0. Mi az a sigmoid transzformáció?

A logisztikus regresszió utolsó lépése, amely a lineáris Score értékeket (log-odds) valószínűségekké (0–1) alakítja át.

1. Miért jó?

• 0–1 közé skáláz bármilyen valós értéket, így közvetlenül értelmezhető valószínűségként.

• Görbe alakja (S-görbe): középen meredek, széleken lapos – érzékeny a határértékeknél, stabil a szélsőértékeknél.

• Differenciálható és egyszerű, ezért jól használható optimizálásra (pl. gradient descent).

• Széles körben támogatott statisztikai és gépi tanulási könyvtárakban (Excel, Python, R, SPSS).

2. Hogyan számítjuk?

• Először kiszámoljuk a logit (F) értéket, azaz a lineáris kombinációt:

  F = w0 + w1*X1 + w2*X2 + … + wn*Xn

• Ebből jön a sigmoid (p):

  p = EXP(F) / (1 + EXP(F)) – ahol EXP(F) = e^F, és p mindig 0 és 1 között lesz.

3. Mikor használd?

• Bináris előrejelzés: igen/nem kimenet (pl. vásárol-e, válaszol-e kampányra, churn‐e).

• Churn-modellek: mekkora eséllyel mondja le az ügyfél az előfizetést?

• Kampány-célzás: kinek érdemes hirdetést vagy e-mailt küldeni?

• Lead scoring: mennyire „meleg” egy potenciális vevő?

4. Marketing-példák

• Kampányválasz előrejelzés
  – X1 = e-mail megnyitási arány; X2 = korábbi vásárlások száma; p = válasz esélye

• Hirdetéskattintás-esély
  – X1 = kattintási history, X2 = oldalmegtekintések; p = kattintás valószínűsége

• Churn-előrejelzés
  – X1 = recency, X2 = frequency, X3 = support calls; p = churn esélye

5. Case Study: E-mailes reakció-optimalizáció

Háttér:
Egy online ruházati webáruház havi hírlevél-kampányt futtat, de a válaszarány csak 8%. Szeretnék növelni a konverziót, miközben csökkentik a kiküldési költséget.

Adatok:

• Minden ügyfélnél ismert az elmúlt 6 hónapban

• X1 = e-mail megnyitási arány (%)

• X2 = vásárlások száma

• X3 = átlagos kosárérték (ezer Ft)

Lépések:

1. Modellépítés:  logisztikus regresszió: F = –4.0 + 0.05*X1 + 0.4*X2 + 0.02*X3

2. Valószínűség számítás:  minden ügyfélre p = EXP(F)/(1+EXP(F))

3. Céllista kiválasztása: csak p > 0.6 ügyfeleknek küldik ki

4. Eredmény:

• Kiküldött e-mailek száma – 30%-kal csökkent

• Válaszarány – 8% → 15%

• ROI javulás – 1,8×

Tanulság:

A sigmoid használatával mérhető, skálázható valószínűségeket kapnak, amik alapján adatalapú döntést hoznak (küszöbérték-optimalizáció), jelentős költségmegtakarítással és jobb megtérüléssel.

6. Mikor ne használd?

• Ha a célváltozó nem bináris, hanem folyamatos vagy többosztályos.

• Ha szeretnénk a szélső (0 vagy 1 közelében) valószínűségeket lineárisan kezelni (a sigmoid belassulhat a csúcsokon).

• Ha a modellezés során nagy F-értékek fordulnak elő és a numerikus stabilitás problémát okoz (overflow).

7. Milyen üzleti kérdésekre adhat választ?

• Ha a marketing igazgató azt kérdezin tőled, hogy “Mekkora eséllyel vásárolnak azok, akik háromszor megnyitották az e-mailünket?”, hogyan válaszolsu?

• A pénzügy azt kéri, állíts be olyan küszöböt, hogy csak 60% feletti esélyű ügyfeleket érjünk el – hogyan omplementálod ezt a gyakorlatba?

• Ha extra ügyfélszolgálati hívásokat iktsz be, mennyivel csökken a kilépési arány?

• Hogyan mutatod be a vezetőségnek, hogy azonos logit értékekből hogyan lesz “p = 0,75” vagy “p = 0,90” valószínűség?

• A kampánycsapat szeretne biztos lenni abban, hogy a 70% feletti vásárlási eséllyel bíró leadeket célozza – hogyan szűrőd ki ezeket?